Java Program For Sum Root to Leaf Numbers

We will be solving LeetCode problem “129. Sum Root to Leaf Numbers” here. This is a common question which has been asked in interview rounds of Google & Microsoft. Problem definition is as follows:

You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.

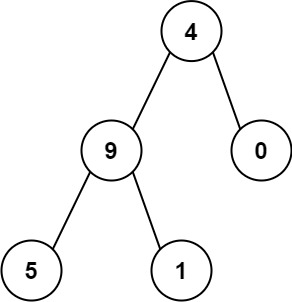
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

The solution looks simple. We will do a depth-first traversal of the binary tree using recursion. We will have two variables. currentSum variable will track the current path. result variable will be used to store sum of all root-to-leaf paths.

• We will add current node value to currentSum variable.
• If current node is not a leaf node, we will recursively call same method for left & right sub-trees with updated currentSum variable.
• If current node is a leaf node, we will add currentSum value to result variable.

Here is the fully working Java code solution of the above problem.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        String currentSum = "";
        //using object instead of primitive to pass & update result in recursive method
        int[] result = new int[1];
        calculateSumRootToLeaf(root, currentSum, result);
        return result[0];
    }
    
    private void calculateSumRootToLeaf(TreeNode node, String currentSum, int[] result){
        currentSum = currentSum + "" + node.val;
        if(node.left == null && node.right == null){
            result[0] = result[0] + Integer.parseInt(currentSum);
        } else {
            if(node.left != null){
                calculateSumRootToLeaf(node.left, currentSum, result);
            }
            if(node.right != null){
                calculateSumRootToLeaf(node.right, currentSum, result);
            }
        }
    }
}

Let’s consider tree size as n. Time complexity of the above solution is O(n). We are just doing a full traversal of tree once.
Space complexity is O(1) if we don’t consider recursion stack. We are just using a couple of extra variables. Number of extra variables doesn’t depend on tree size.