We will solve Median of two sorted arrays problem here. It is a common problem solving question which is asked in interview rounds of companies like Amazon, Google, Microsoft & Goldman Sachs. We will use LeetCode problem “4. Median of Two Sorted Arrays” as example here. The problem states that:
Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example 1:
Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.
Example 2:
Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
If you read through the above problem statement, you will see that the ask is to solve the problem in O(log (m+n)) time complexity.
We could have done this in O(m + n) time complexity easily. We could have merged the two sorted arrays into a single one. That would be the merging step of Merge Sort algorithm. We could have done it in O(m + n) time. Once we have the merged array, we can find the median in O(1) time as we know the array size. But linear time complexity is not sufficient. We need to reduce the complexity to logarithmic value.
So how can we achieve logarithmic time complexity?
First thing first. We still know where the median lies as we know the array size. Suppose array size is n. For array with odd number of elements, it would be (n / 2) + 1 element. In first example, array has 3 elements & median is 2nd element. For array with even number of elements, there are two median elements, n / 2 & (n / 2) + 1. In second example, array has 4 elements & median elements are 2nd & 3rd elements.
As we know the median, we also know the total number of elements that should be on the left hand side of median. All left hand side elements of median should be less than the right hand side elements. In our case, left hand side elements till median might spread across the two arrays. Our goal is to find the correct partitions from both arrays which will give all left side elements till the median in the merged array.
We will take the smaller array & find its middle element. Suppose smaller array size is m & bigger array size is n. So we have taken m / 2 left elements from smaller array. Remaining ((m + n) / 2 + 1) – (m / 2) elements will be taken from left hand side of bigger array. Now we need to do two additional checks.
- The current partition element of smaller array should be less than the first element of right partition in bigger array.
- Same way, partition element of bigger array should be less than the first element of right partition in smaller array.
In case partition element in smaller array is greater than the first element of right partition in bigger array, we will move to the left half of smaller array & find middle element of it.
In case partition element of bigger array is greater than the first element of right partition in smaller array, we will move to the right half of the smaller array & find next middle element from it.
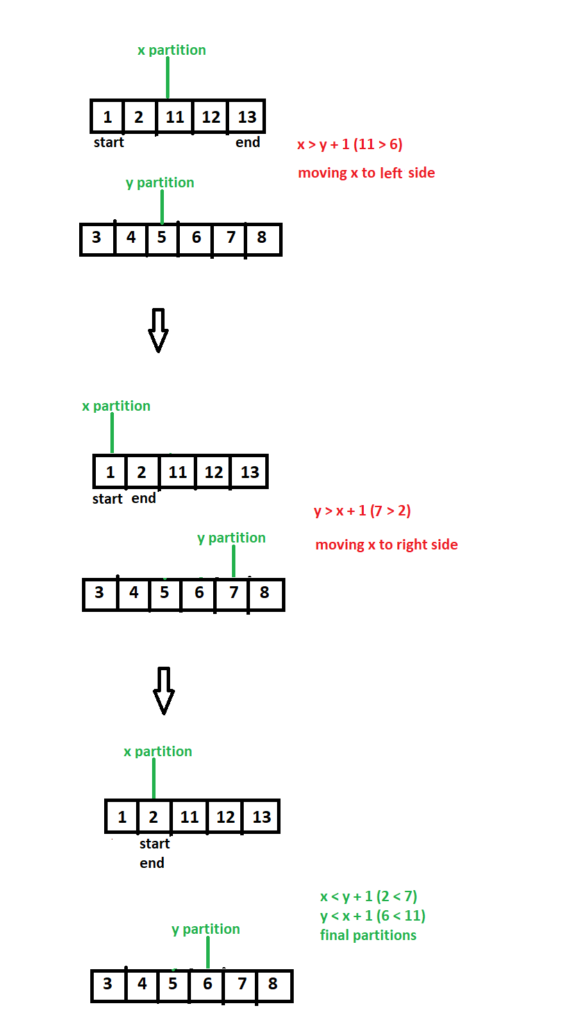
You can see the process in the above diagram. Basically we are doing a kind of binary search. Once both the additional checks satisfy, we have found correct partitions. We can find the median elements from there. The time complexity of finding the median is O log m. Or if we don’t know which array is smaller, time complexity of the above solution can be written as O (log (min(m, n))).
The complete Java solution of the above LeetCode problem is given below.
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if(nums1.length > nums2.length){
return findMedianSortedArrays(nums2, nums1);
}
int start = 0;
int end = nums1.length - 1;
while(start <= end){
int nums1Partition = (end + start) / 2 ;
int nums2Partition = (nums1.length + nums2.length - 1) / 2 - nums1Partition - 1;
int nums1RightValue = nums1Partition == nums1.length - 1 ? Integer.MAX_VALUE : nums1[nums1Partition + 1];
int nums2RightValue = nums2Partition == nums2.length - 1 ? Integer.MAX_VALUE : nums2[nums2Partition + 1];
int nums1LeftValue = nums1Partition < 0 ? Integer.MIN_VALUE : nums1[nums1Partition];
int nums2LeftValue = nums2Partition < 0 ? Integer.MIN_VALUE : nums2[nums2Partition];
if(nums1LeftValue <= nums2RightValue && nums2LeftValue <= nums1RightValue){
if((nums1.length + nums2.length) % 2 == 1){
return Math.max(nums1LeftValue, nums2LeftValue);
} else {
return (Math.max(nums1LeftValue, nums2LeftValue) +
Math.min(nums1RightValue, nums2RightValue)) / 2.0;
}
} else if(nums1LeftValue > nums2RightValue){
end = nums1Partition - 1;
} else {
start = nums1Partition + 1;
}
}
int totalSize = nums1.length + nums2.length;
// either nums1 is empty or all nums2Partition elements are less than starting element of nums1
if(totalSize % 2 == 1) {
return nums2[totalSize / 2];
} else {
int leftValue = nums2[(totalSize - 1)/ 2];
int rightValue = (totalSize / 2) == nums2.length ? Integer.MAX_VALUE : nums2[totalSize / 2];
if(nums1.length > 0 && nums1[0] < rightValue) {
rightValue = nums1[0];
}
return (leftValue + rightValue) / 2.0;
}
}
}