We will try to find all possible permutations of a given string. To understand this problem, we will use “LeetCode problem 47. Permutations II” and solve it. The problem states that:
Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.
Input: nums = [1,1,2] Output: [[1,1,2], [1,2,1], [2,1,1]]
The above LeetCode problem has one extra requirement. There can be duplicate numbers in the collection, but the permutations returned should be unique. We will come to the unique part later. We will first understand how to find all possible permutations of a given collection of size n.
Let’s say we have three distinct characters A, B, C in a collection. We will find all possible permutations of these three characters.
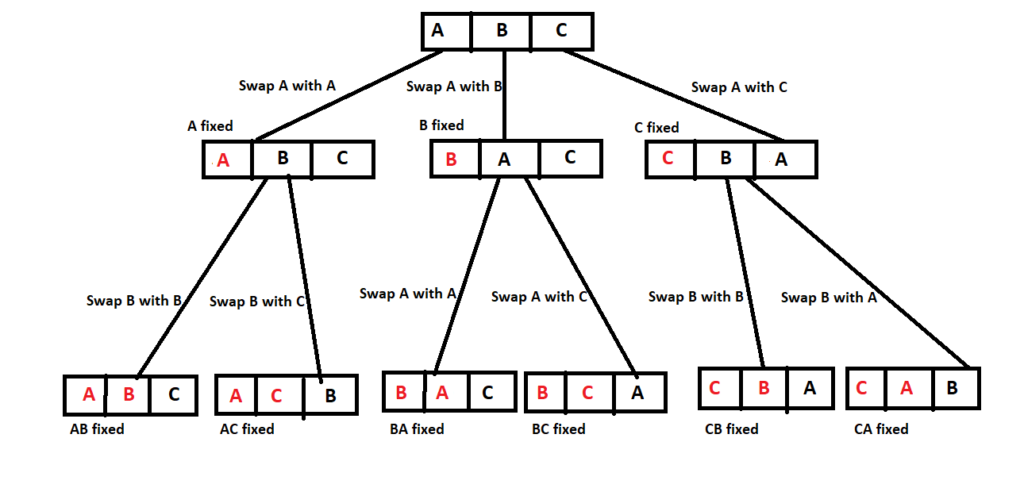
We will start a loop from 0th index element and swap all elements with it. That way we will get a different character (A, B or C) at each iteration. Once we swap element, we will make recursive call on the remaining n-1 characters. Suppose A is fixed at 0th index. So in first recursive call, we will start a loop at 1st index & swap all elements till end with it. That way, we will get a different character (B or C) at 1st index in each iteration of the loop within first recursive call. We will continue recursive call till we traverse total n characters in the recursion tree. Once we reach n characters, then we have found one of the permutations. You can refer to the recursion tree in the diagram above to better understand how this works.
This is simple backtracking process where we do depth-first traversal with recursion. For example, we swap 0th element with 1st element. Then we make the recursive calls with original 1st element in 0th position. Once we find all permutations with original 1st element in 0th position, we backtrack by swapping current 0th element with current 1st element to go back to previous original state. Next we do the swapping of 0th element with 2nd element.
Now we understood how to find all permutations from a given collection. To find unique permutations where collection contains duplicate characters, we will use a HashSet when we start the loop. At each iteration, we will check if current element is already present in the set or not. If it already exists, we have a duplicate & swapping current element will give us same permutations we already encountered previously. So we will skip the recursive calls for this element & go to the next one.
Here is the complete Java code solution for the above LeetCode problem.
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<Integer> currentResult = new ArrayList<Integer>();
List<List<Integer>> results = new ArrayList<List<Integer>>();
int startPosition = 0;
calculate(nums, startPosition, results);
return results;
}
private void calculate(int[] nums, int startPosition,
List<List<Integer>> results) {
if(startPosition == nums.length - 1){
List<Integer> currentResult = new ArrayList<Integer>();
for(int num : nums){
currentResult.add(num);
}
results.add(currentResult);
}
else {
Set<Integer> usedNumbers = new HashSet<Integer>();
for(int i = startPosition; i < nums.length; i++){
if(usedNumbers.contains(nums[i])){
continue;
} else {
usedNumbers.add(nums[i]);
swap(nums, startPosition, i);
calculate(nums, startPosition + 1, results);
//backtracking
swap(nums, startPosition, i);
}
}
}
}
private void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}Let’s calculate time complexity of the solution.
T(n) = n * T(n-1) T(n-1) = (n-1) * T(n-2) T(n-2) = (n-2) * T(n-3)
As you can see time complexity becomes n * (n-2) * (n – 3) … * 1 which is O(n!).