Quick Sort is a notable sorting algorithm. I will try to explain Quick Sort in simple terms. Let’s take an example:
Input: 12 25 14 30 15 Output: 12 14 15 25 30
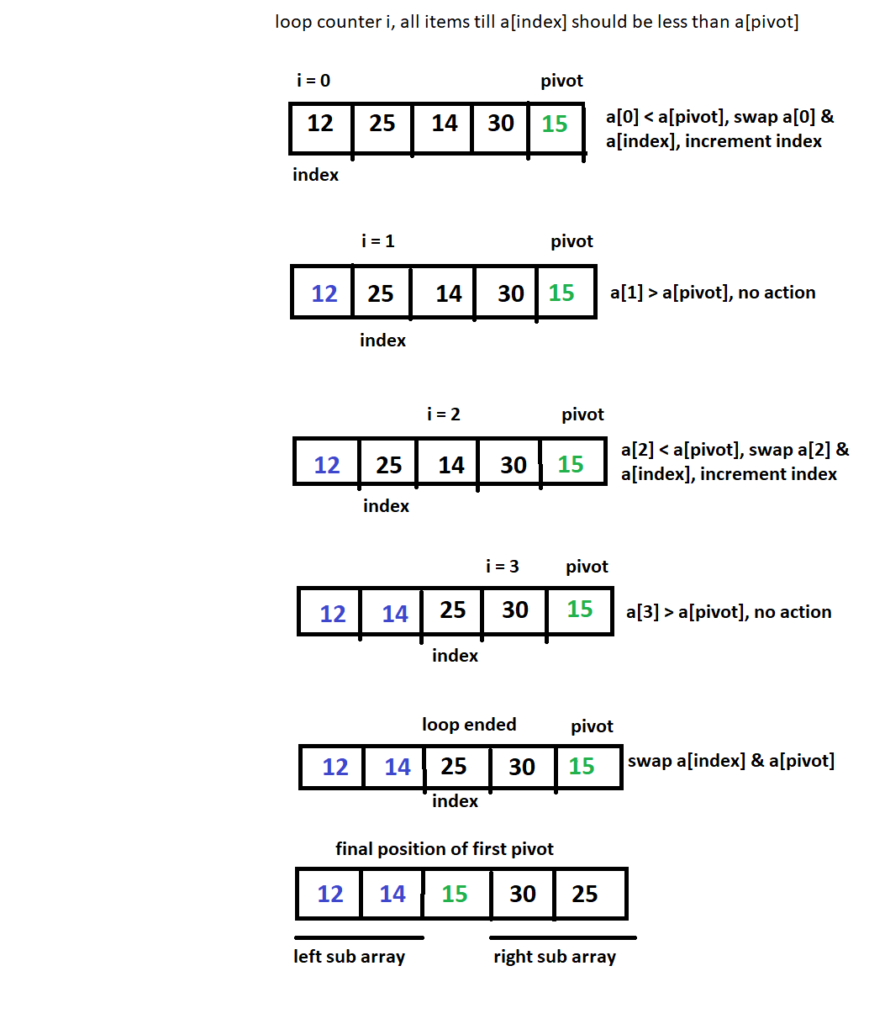
Suppose we have an unsorted array [12, 25, 14, 30, 15] as mentioned above. We will sort the unsorted array using Quick Sort algorithm.
Quick Sort works in different phases:
Pivot Selection: We select any element in the array as pivot. We can select any random element as pivot (more about that below). Let’s say we take right-most element as pivot for our example.
Re-arrange elements based on the Pivot: Next step is to arrange the other elements in the array around the pivot. All elements with lower value than pivot should be on the left hand side of the pivot and higher value elements should be on the right hand side of the pivot. Then we know that pivot has been placed to its final correct position. It will remain there even when the full array is sorted. Remember, left hand side elements of the pivot are not yet sorted among themselves. They are just less than the pivot element. Same goes for the right hand side elements of pivot. They are not sorted among themselves. They are just greater than the pivot.
Advantage of doing this is that we have found the final position of one element in linear time. Rearranging elements based on pivot value can be done in linear time using a while loop & swapping. You can find the Java implementation of the method at the bottom of the post.
Apply Recursion on left & right sub-arrays: Now we have one element in its final position. We can apply above steps recursively on the left hand side array & the right side array. Recursion stops when we reach a state where each sub-array contains only one element. Single element array is already sorted, no further action is required.
What is the time complexity of this algorithm? The time complexity of finding the final sorted position of first pivot is n. So at first look, we might assume that for n pivots it would take n * n = n ^ 2 time. That is not necessarily true. It depends on the final position of the pivot & whether it divides the array in two equal halves.
Time Complexity Example 1:
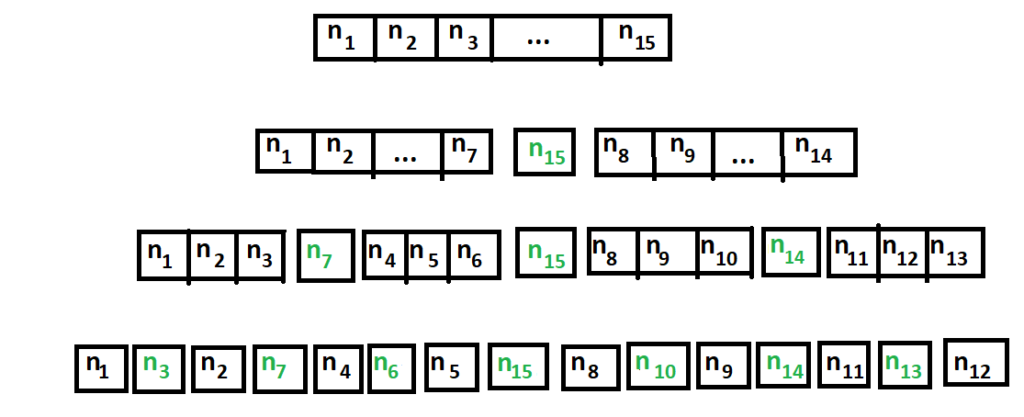
If you see above diagram, at each recursion step array is getting divided into two equal halves. At first recursion level, we found position of one pivot with n comparisons. At 2nd recursion level, we found positions of two new pivots with total n-1 comparisons (left n – 1 / 2 + right n-1 / 2). In 3rd recursion level, we found positions of four new pivots with total n-3 comparisons. So it is not true that at each recursion level we can get position of only one pivot. Suppose recursion tree height is h. If you follow the pattern as mentioned above, we can write the equation as:
2 ^ 0 + 2 ^ 1 + 2 ^ 2 + … + 2 ^ h = n
2 ^ (h + 1) – 1= n
2 ^ (h + 1) = n + 1
h + 1 = log base 2 (n + 1)
h = log (n + 1) – 1
So height of recursion tree is log (n + 1) – 1. At each recursion level, max number of comparisons would be n or less. So time complexity of this example would be O(n log n).
Time Complexity Example 2:
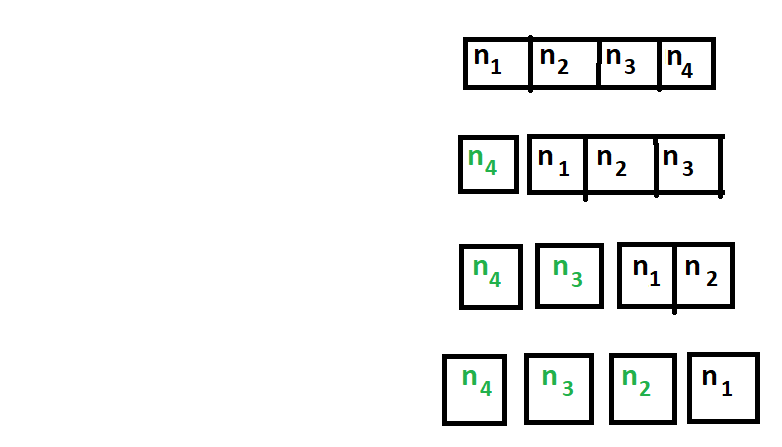
Here at first recursion level, pivot is placed at the beginning. So there is no left hand array & we have only right hand array. At next recursion level, the new pivot again gets placed at the beginning of the sub-array. So there is no left array. This goes on. So number of recursion level is n. And at each recursion level, maximum number of comparisons gets decremented by 1. You can see it in the above diagram.
Time complexity:
n + (n – 1) + (n – 2) + …. + 1
= n * (n + 1) / 2
= O(n ^ 2)
From these two examples you can see that the average time complexity of Quick Sort is O(n log n) & the worst time complexity is O(n ^ 2). Basically time complexity depends on how the unsorted array is distributed initially & the technique we choose for pivot selection. There are various techniques for pivot selection which help in dividing the array in somewhat equal halves. May be I will write a post about that in future. But I hope the basic concept of Quick Sort is clear now.
Here is the complete Java code solution for Quicksort:
// { Driver Code Starts
import java.util.*;
class Sorting
{
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i]+" ");
System.out.println();
}
// Driver program
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
while(T>0)
{
int n = sc.nextInt();
int arr[] = new int[n];
for(int i=0;i<n;i++)
arr[i] = sc.nextInt();
new Solution().quickSort(arr,0,n-1);
printArray(arr);
T--;
}
} }// } Driver Code Ends
class Solution
{
//Function to sort an array using quick sort algorithm.
static void quickSort(int arr[], int low, int high)
{
if(low >= high){
return;
}
int sortedIndex = partition(arr, low, high);
quickSort(arr, low, sortedIndex - 1);
quickSort(arr, sortedIndex + 1, high);
}
static int partition(int arr[], int low, int high)
{
int pivot = high;
/* keeps track of the current index where left-hand side
elements are less than pivot element*/
int index = low;
for(int i=low; i < high; i++){
if(arr[i] < arr[pivot]){
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index);
return index;
}
private static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}