I have seen people getting confused about how a binary heap can be built in O(n) time complexity. There are online articles & videos regarding this. I will try to explain it in my own way as simply as possible.
First thing first, a binary heap is a complete binary tree. All levels of complete binary tree must be completely filled except the last level. That means leaf nodes can be present only at the last level & the level above. Binary heap can be a min-heap or max-heap. For mean-heap, parent should be less than all the nodes in left & right sub-trees. For max-heap, parent should be greater than all the nodes in left & right sub-trees.
Complete Binary Tree Example 1: All levels are completely filled.
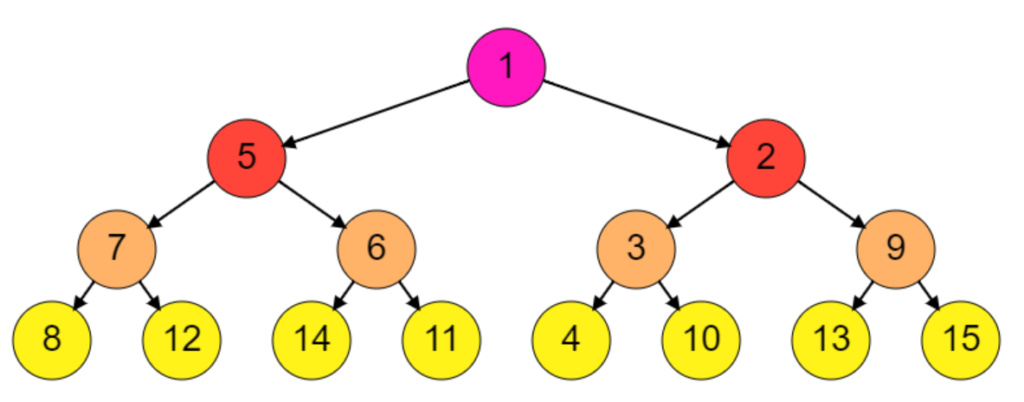
level 0, nodes = 2 ^ 0 = 1 level 1, nodes = 2 ^ 1 = 2 level 2, nodes = 2 ^ 2 = 4 level 3, nodes = 2 ^ 3 = 8
Level 3 contains all the leaf nodes. Total leaf node count is 8. Total non-leaf node count is (1 + 2 + 4) = 7. So total leaf node count is one more than the total non-leaf node count. This will be true for any number of levels as long as the complete binary tree is completely filled.
Complete Binary Tree Example 2: Last level is partially filled.
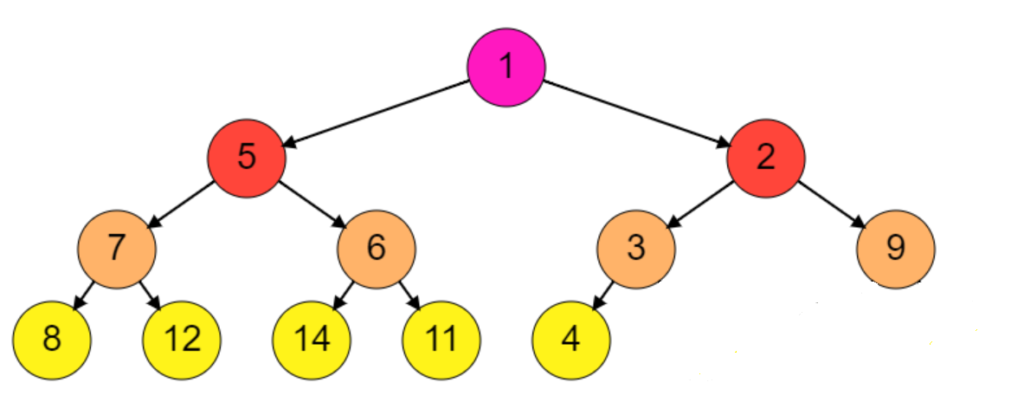
level 0, nodes = 2 ^ 0 = 1 level 1, nodes = 2 ^ 1 = 2 level 2, nodes = 2 ^ 2 = 4 level 3, nodes = 2 ^ 3 = 5
Level 2 has 1 leaf node & level 3 has 5 leaf nodes. Total leaf node count is (1 + 5 = 6). Total non-leaf node count is (1 + 2 + 3 = 6). So leaf node count & non-leaf node count is equal. For any complete binary tree where last level is partially filled, leaf node count will be same or greater than non-leaf node count.
From the above two examples, we know that at least half of the nodes will be leaf nodes in a binary heap. This is an important thing to understand.
There are two ways to build a heap. One is top-down approach. Another is bottom-up approach. We have an array of integers [7, 6, 5, 4, 3, 2, 1]. We will build min-heap from these elements. The array contains the elements in reverse order so that we can simulate worst case scenario.
Top-Down Approach:
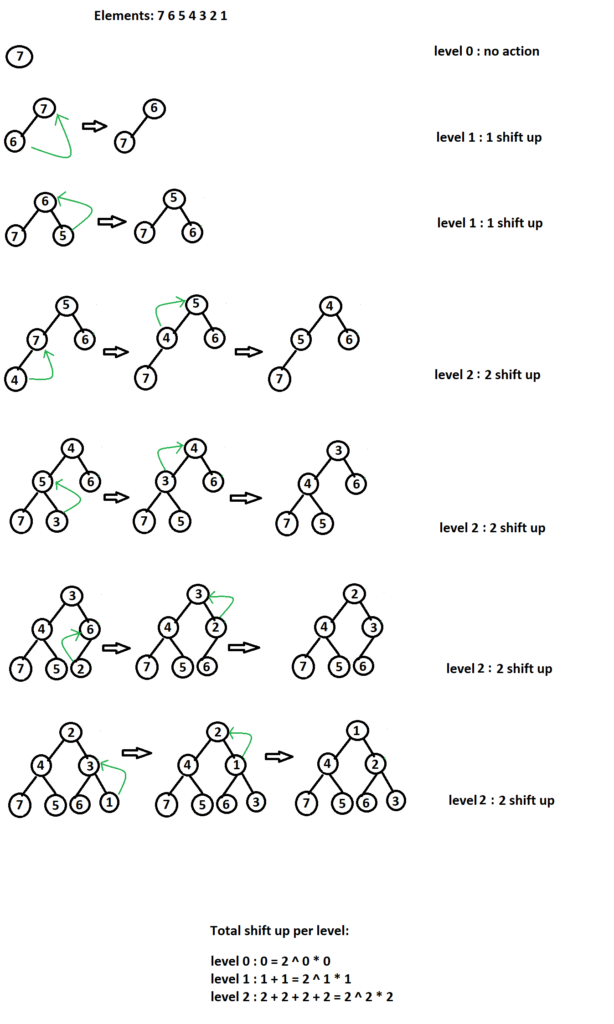
It is also called shift-up approach. We take an empty heap. Then we start inserting element from the root & keep on inserting elements in the next levels one by one. Inserted elements might bubble up to satisfy heap property as you can see from the diagram above. We can also see that all the nodes which get inserted at leaf level might bubble up till root level to satisfy heap property. We already know at least half of the nodes are leaf nodes in a binary heap. So we might need to shift n / 2 elements from leaf level to root level. The distance between last level to root level is height (h) of tree which is log n in case of complete binary tree. So in worst case scenario, we would need to make (n / 2) * log n shift-up for leaf nodes. So worst case time complexity can’t be less than O(n log n). It is not linear. Top-down approach doesn’t construct binary heap in O(n) time complexity. Here worst case time complexity in O(n log n).
Bottom-Up Approach:
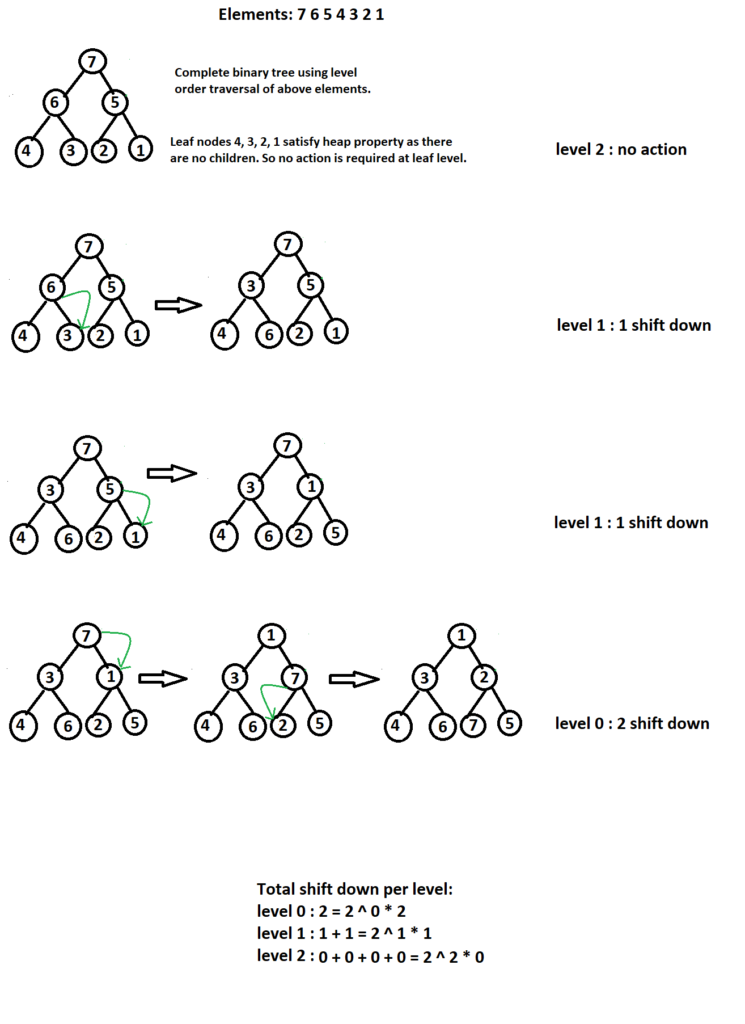
It is also called shift-down approach. First we will create a complete binary tree using level order traversal. But if you see the diagram above, this complete binary tree doesn’t satisfy min-heap property. We will have to convert it to a min-heap. We will start from the last level. If we consider each leaf node individually, each of them is a min-heap by itself as there are no children in a leaf node. So no action is required for leaf nodes. We can go one level up. We might have to shift down the elements to satisfy heap property. Let’s say height of heap is h. So at (h-1) level, we can shift down maximum 1 level. At (h-2) level, we can shift down maximum 2 levels. At root level, we can shift down maximum h level to satisfy heap property. You can get a clear idea if you see the above diagram. So we can write something similar as below:
(0 * n / 2) + (1 * n / 4) + (2 * n / 8) + (3 * n / 16) + … + (h * 1) = (0 * n / 2 ^ 1) + (1 * n / 2 ^ 2) + (2 * n / 2 ^ 3) + (3 * n / 2 ^ 4) + … + (h * 1) = (0 * n / 2 ^ 1) + (1 * n / 2 ^ 2) + (2 * n / 2 ^ 3) + (3 * n / 2 ^ 4) + … + (h * n / 2 ^ (h + 1)) = 0 + (1 * n / 2 ^ 2) + (2 * n / 2 ^ 3) + (3 * n / 2 ^ 4) + … + (h * n / 2 ^ (h + 1)) = (1 * n / 2 ^ 2) + (2 * n / 2 ^ 3) + (3 * n / 2 ^ 4) + … + (h * n / 2 ^ (h + 1)) = n * ((1 / 2 ^ 2) + (2 / 2 ^ 3) + (3 / 2 ^ 4) + … + (h / 2 ^ (h + 1)))
Now for any value of h (even when h approaches infinity), (1 / 2 ^ 2) + (2 / 2 ^ 3) + (3 / 2 ^ 4) + … + (h / 2 ^ (h + 1)) will never exceed 1.
So worst time complexity of building binary heap using bottom-up approach is O(n). If we consider the time complexity of building the initial complete binary tree, that would be O(n). So total time complexity of building the initial complete binary tree & converting it to binary heap is n + n = 2n which again becomes O(n). By the way, array itself can represent a complete binary tree. I just used the actual binary tree representation for explaining the heap construction completely.
So as you can see, bottom-up approach can be used to build a binary heap at O(n) time complexity.