We are here to solve a LeetCode problem “166. Fraction to Recurring Decimal“. The problem states that:
Given two integers representing the numerator and denominator of a fraction, return the fraction in string format. If the fractional part is repeating, enclose the repeating part in parentheses.
Non-repeating Sequence Example: Input: numerator = 1, denominator = 2 Output: "0.5"
Repeating Sequence Example: Input: numerator = 4, denominator = 333 Output: "0.(012)"
The problem looks simple, at least for non-repeating case. We can do a division for the given two numbers & get the fraction value. But the repeating example looks a bit tricky. There are few questions that we need to find solutions for:
- How do we identify that the fraction has repeating sequence?
- How do we find the starting point of the repeating sequence if any?
These might also sound simple at a quick glance. We might think that if any digit repeats itself in the fraction, then the fraction has a recurring sequence. And the first occurrence of the digit is the starting point of the recurrence. This assumption is wrong. Let’s consider this example:
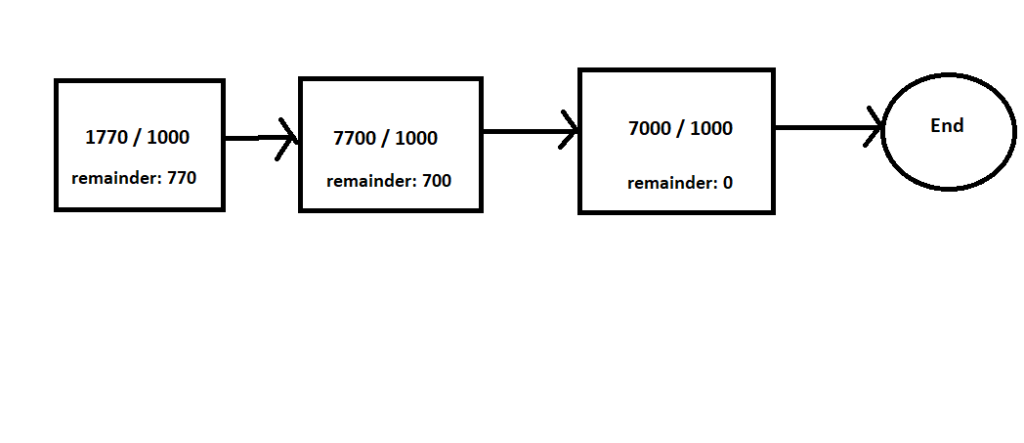
Input : numerator = 177, denominator = 1000
177 / 1000 = 0 177 % 1000 = 177
Now we need to calculate the fraction part. The process is simple. Let’s just refresh it in case some of us have forgotten it.
- Remainder = remainder * 10.
- Append remainder / denominator to previous result.
- Remainder = remainder % denominator.
- Repeat steps 1 to 3 till remainder becomes 0.
Loop 1: 177 * 10 = 1770 1770 / 1000 = 1 So current result is 0.1. 1770 % 1000 = 770
Loop 2: 770 * 10 = 7700 7700 / 1000 = 7 After appending 7 to previous result, current result becomes 0.17. 7700 % 1000 = 700
Loop 3: 700 * 10 = 7000 7000 / 1000 = 7 After appending 7 to previous result, current result becomes 0.177. 7000 % 1000 = 0
Reminder is 0, so final result is 0.177.
The digit 7 got repeated once. But it is not a repeated/recurring sequence. The fraction part just ends there. This proves that our assumption was wrong that repeated digit starts a repeating sequence.
Then how do we figure out if the fraction contains a recurring sequence? We need to think in terms of numerator state instead of a fraction digit. We need to check current numerator state at each loop iteration. Denominator is always same. So if we get same numerator that we already encountered previously, then we would again do the same division that we already did. So same series of subsequent steps will bring us back to this state again & again. It would be a never ending loop.
In above example, numerator states are 1770, 7700, 7000. All three are different.
Let’s take a recurring sequence example next.
Input : numerator = 5, denominator = 33
5 / 33 = 0 5 % 33 = 5
We will calculate the fraction part.
Loop 1: 5 * 10 = 50 50 / 33 = 1 Now we have 0.1. 50 % 33 = 17
Loop 2: 17 * 10 = 170 170 / 33 = 5 So now we have 0.15. 170 % 33 = 5
Loop 3: 5 * 10 = 50
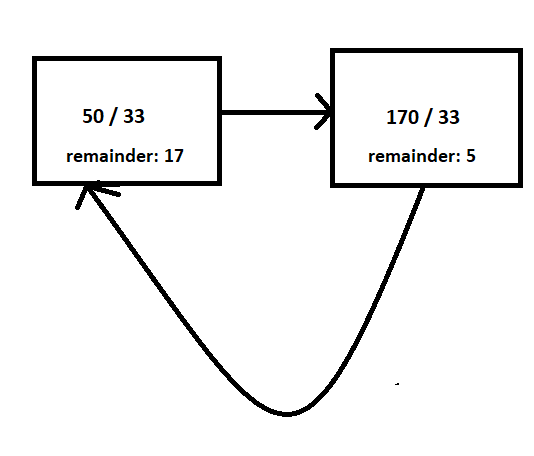
But we already had 50 as numerator in loop 1 & we have already done 50 / 33 there. So if you just think through, we have come back to a previous state with same numerator & denominator. So we know if we do state transitions using same division operation, we will come back to this state again.
As we found numerator state is repeating, we can safely say we have found a recurring sequence.
Now what is the starting point of the repeating sequence? It is the same state where we found the initial match. In above example, it is 50.
So the answer is 0.(15).
Now we need to translate this logic into Java code. We will use a HashMap to store numerator value at each iteration along with current position after decimal point. Also at each iteration within the loop, we will check if current numerator is already present in the HashMap or not. If numerator already exists in the map, we have found a recurring fraction sequence. Here is the complete working Java solution for this problem:
class Solution {
public String fractionToDecimal(int numerator, int denominator) {
StringBuilder result = new StringBuilder();
// to handle scenario when either numerator or denominator is negative
if((numerator > 0 && denominator < 0) || (numerator < 0 && denominator > 0)){
result.append("-");
}
//first convert to long & then get absolute value
//else int -2147483648 would give incorrect absolute value (beyond int max value)
long num = numerator;
long den = denominator;
num = Math.abs(num);
den = Math.abs(den);
long quotient = num / den;
result.append(quotient);
long remainder = num % den;
if(remainder == 0){
return result.toString();
}
result.append(".");
Map<Long, Integer> fractionDigitPositionMap = new HashMap<Long, Integer>();
int currentPosition = 0;
while(remainder > 0){
num = remainder * 10;
if(fractionDigitPositionMap.containsKey(num)){
int intialPosAfterDecimalPoint = fractionDigitPositionMap.get(num);
int decimalPointPosition = result.indexOf(".");
result.insert((decimalPointPosition + intialPosAfterDecimalPoint), "(");
result.append(")");
break;
}
fractionDigitPositionMap.put(num, ++currentPosition);
quotient = num / den;
result.append(quotient);
remainder = num % den;
}
return result.toString();
}
}As you can see from the code above, worst time complexity is linear.