Java Program for Least Common Ancestor Of A Binary Tree

We will solve LeetCode problem “236. Lowest Common Ancestor of a Binary Tree” here. The problem states that:

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

All node values are unique. Also p and q will always exist in the tree.

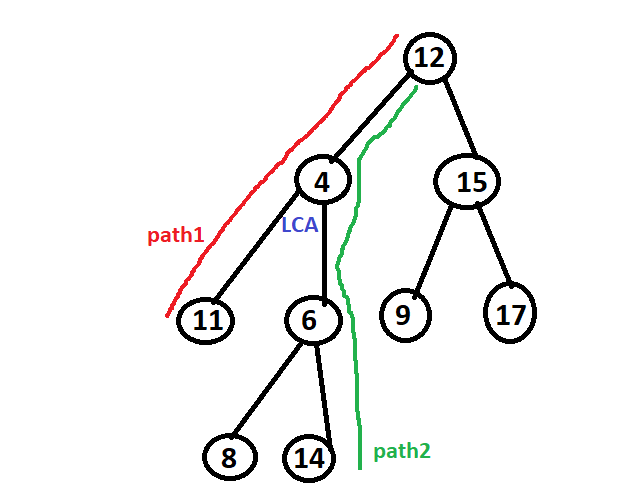
Input: root = [12, 4,15, 11, 6, 9, 17, null, null,8, 14], p = 11, q = 14
Output: 4
Explanation: The LCA of nodes 11 and 14 is 4.

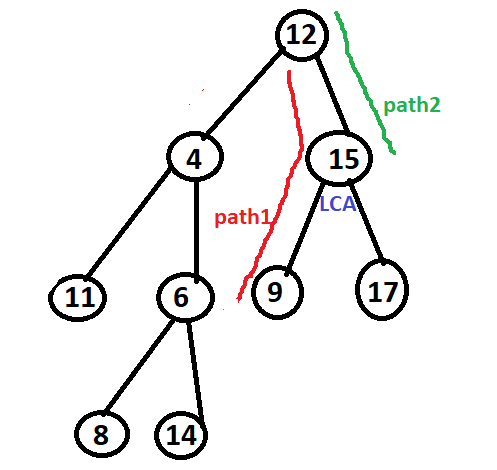
Input: root = [12, 4,15, 11, 6, 9, 17, null, null,8, 14], p = 9, q = 15
Output: 15
Explanation: The LCA of nodes 9 and 15 is 15. A node can be a descendant of itself as per the LCA definition.

Solution: We will be traversing the tree twice separately, once for finding p & another time for finding q. We will store paths to p & q in two ArrayList variables. Once we have calculated both the paths, we will compare the elements of the ArrayList variables with each other one by one. We will stop at the first element where there is a diversion or the value is equal to p or q. That will give us the LCA or lowest common ancestor for these two nodes within the binary tree.

Time Complexity: Suppose binary tree size is n. We are doing two traversals of the tree to find paths for p & q nodes. We are also comparing two path variables with each other. Path variable size can be up to n. In total there are two traversals of n elements & one comparison of n elements. That is 3n. So time complexity of the above solution would be O(n) if we remove the constant part.

Space Complexity: We are using two extra ArrayList variables whose size can be up to n. So at most 2n extra space would be used. So space complexity of the above solution is O(n).

Here is the fully working Java code solution of the above LeetCode problem.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> path1 = new ArrayList<TreeNode>();
        List<TreeNode> path2 = new ArrayList<TreeNode>();
        
        findPathToValue(root, path1, p);
        findPathToValue(root, path2, q);
        
        int smallerSize = Math.min(path1.size(), path2.size());
        
        int i=0;
        for(;i<smallerSize; i++){
            if(!path1.get(i).equals(path2.get(i))){
                break;
            }
        }
        
        return path1.get(i - 1);
    }
    
    private boolean findPathToValue(TreeNode current, List<TreeNode> path, TreeNode target){
        path.add(current);
        if(current.val == target.val){
            return true;
        }
        if(current.left != null && findPathToValue(current.left, path, target)){
            return true;
        }
        if(current.right != null && findPathToValue(current.right, path, target)){
            return true;
        }
        path.remove(path.size() - 1);
        return false;
    }
}

There is a solution where we can find LCA with a single traversal of the binary tree. But I intentionally didn’t show it here. For single traversal solution to work, p & q both need to exist. There is a variant of the above problem where p or q might not exist in the binary tree. In that case, lowest common ancestor would be -1. We can easily extend our solution to cover that scenario as well as shown below. Time & space complexities still remain same.

        findPathToValue(root, path1, p);
        findPathToValue(root, path2, q);
        if(path1.size() == 0 || path2.size() == 0){
            return -1;
        }